My first decade of teaching mathematics in the 1980’s consisted of using worked-out examples and emphasizing memorized procedures. My teaching was similar to what I had experienced as a student.
But then, the 1991 NCTM Professional Teaching Standards showed me a vision of teaching in a different, more powerful way and inspired me to revamp my teaching methodology. However, I soon found that implementing tasks designed to elicit mathematical thinking and discussion was often very difficult.Using a student’s own work as a tool for learning mathematics challenged my own instructional beliefs. Not only did I have to admit that I wasn't the only mathematician in the classroom, I had to believe, and admit, that sometimes my students' insights and strategies were as good or better than my own. I also found that my own mathematical thinking wasn’t very flexible, particularly as my students’ insights and strategies varied from my own.
Perhaps you have, or will, experience similar challenges as you engage in the Open Up High School Mathematics curriculum with your students. Perhaps, like me, you will be tempted to give up before really giving yourself, and your students, an opportunity to grow mathematically. The framework that breathed new life into my initial failed attempts at task-based instruction appeared first as a journal article: Orchestrating Productive Mathematical Discussions: Five Practices for Helping Teachers Move Beyond Show and Tell (Stein, et al. 2008), and was later fleshed out in a an enlightening book: 5 Practices for Orchestrating Discussions (Smith and Stein, 2011).
A classroom filled with groups of students actively engaging in cognitively demanding problems using a variety of methods and representations can feel overwhelming, especially as the teacher tries to attend to the emerging mathematical ideas and strategies of each individual student. Making decisions, in the moment of teaching, regarding which examples of student work to use to meet the goals of a lesson can be influenced more by rushed decisions than by careful planning. The resulting discussion often ends up as an unstructured “show and tell” activity, instead of a discussion focused on creating shared understanding among the class members. The five practices are intended to overcome the management issues that often plagued my initial attempts at task-based instruction.
This table summarizes what I learned about the five practices and how they support students in making sense of mathematics:
|
The practice and when it happens |
How the practice supports mathematical thinking and mathematical discourse |
|
1. Your lesson preparation begins as you anticipate student thinking. |
You are better prepared to attend to the visual, written or spoken discourse of the students if you first anticipate possible pathways for solving the problems that will be given to your students. |
|
2. After launching students into a challenging problem, you should monitor student thinking as they engage in the task. |
You monitor by observing, by asking questions to help students describe what they are doing and why, or by asking questions to prompt students to revise their work. |
|
3. After noting the work of several individuals or groups of students, select student thinking to be shared with the whole class. |
As you invite students to present, provide time for them to rehearse what they will say and how they will make their thinking visible through words, symbols and other representations. |
|
4. Once student work samples have been selected, sequence student thinking into an accessible order of ideas, strategies and representations that will build towards the goals of the lesson. |
When student work is thoughtfully sequenced, students will naturally draw upon the work of prior presenters to clarify or deepen their own explanations. |
|
5. As students present their work and examine the work of their peers, you can connect student thinking by asking students to note similarities and differences in the strategies and representations presented and by helping them notice the conceptual and procedural thinking that has been generated by the task. |
Many students can contribute a portion of their mathematical work to the whole class discussion—a diagram, a question, or a potential result—without having a complete solution or argument; and they will note how their thinking contributes to the flow of shared mathematical ideas and strategies that will form the “takeaways” of the lesson. |
In the Open Up High School Mathematics Teacher Guide: 5 Practices Charts the authors have provided examples of how these practices might play out for each lesson. The Anticipate and Monitor charts provide insights into potential strategies and representations students commonly use, and describe how to engage students in a small group mathematical discussion using questions. As part of your lesson preparation, you are encouraged to add strategies to the chart that you anticipate your students might use based on your awareness of their mathematical understanding. You might also add questions that prompt students toward deeper mathematical thinking or cause them to revise or refine their thinking. During the Explore phase of the lesson the charts can be used to make note of which students are engaging in anticipated ways of thinking, allowing you to focus more closely on what is right in unanticipated student work or what misconceptions are getting in the way. The charts also propose possible questions to prompt students to adapt or deepen their thinking.
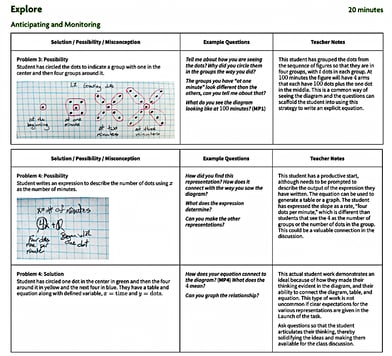The Select, Sequence and Connect charts suggest a possible set of student work that can be used to develop the goals of the lesson and the order in which the mathematical story of the lesson might unfold. These charts suggest questions to be used to support the student-presenters in clarifying their thinking for the class and questions for drawing the remainder of the students into the conversation of making sense of each unique contribution of their peers.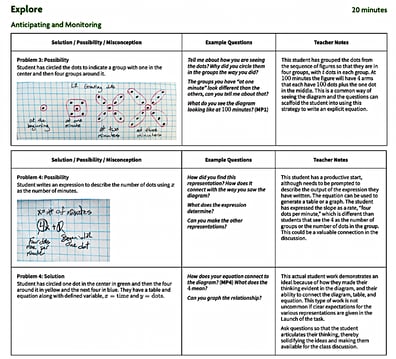
Since the 1998 release of the five practices, a 0th practice has been added—Identify the purpose or goals of the lesson that will be the focus of the whole class discussion. It became apparent that the five practices could only be enacted in the light of the intended learning outcomes of the lesson.
I would also suggest adding a 6th practice to your repertoire: Reflect on student thinking. This practice would occur after the lesson is over and the students have left the classroom, leaving the artifacts of their thinking behind. This is an appropriate time to record additional student work on the Anticipate and Monitor chart for reference in future implementations of the lesson. In these quiet and reflective moments, you will notice new things in your students’ work. Perhaps you will identify a strategy or representation that would have clarified some of the goals of the lesson better than the ones initially selected for the whole class discussion. Perhaps some student work will reveal interesting new insights into the conceptual understanding of a procedure or interesting ways of keeping track of mathematical ideas.
I find that as I consistently do this reflective work I become more confident in the mathematical thinking of my students. This practice also decreases my concerns about relinquishing the role of being the sole mathematical authority in the classroom.
References
Smith, Margaret, and Mary Kay Stein. 2011. 5 Practices for Orchestrating Productive Mathematics Discussions. Reston, VA: National Council for Teacher of Mathematics.
Stein, Mary, Randi Engle, Margaret Smith, Elizabeth Hughes. 2008. “Orchestrating Productive Mathematical Discussions: Five Practices for Helping Teachers Move Beyond Show and Tell.” Mathematical Thinking and Learning 10: 313-340.
Scott Hendrickson recently retired after serving 14 years as a teaching professor in the Department of Mathematics Education at Brigham Young University. Previous to this assignment, he taught for 26 years in public education as a high school mathematics teacher. For 8 of those years he also served as a K-12 district math specialist. He is a past president of the Utah Council of Teachers of Mathematics and served 7 years on the UCTM board. Scott is a co-author of articles appearing in Teaching Children Mathematics, Mathematics Teaching in the Middle School, and Teachers Engaged in Research: Inquiry into Mathematics Practice, grades 9-12. He was the 1994 Utah Teacher of the Year, and a recipient of the 2003 Presidential Award for Excellence in Mathematics and Science Teaching. Scott currently serves as an author and consultant for Mathematics Vision Project and the newly released Open Up High School Mathematics curriculum published by Open Up Resources.
